알고리즘들 중에는, 재귀 알고리즘 (recursive algorithm) 이라고 불리는 것들이 있습니다. 이것은 알고리즘의 이름이 아니라 성질입니다. 주어진 문제가 있을 때, 이것을 같은 종류의 보다 쉬운 문제의 답을 이용해서 풀 수 있는 성질을 이용해서, 같은 알고리즘을 반복적으로 적용함으로써 풀어내는 방법입니다.
예를 들면, 1 부터 n 까지 모든 자연수의 합을 구하는 문제 (sum(n))는, 1 부터 n - 1 까지의 모든 자연수의 합을 구하는 문제 (sum(n - 1))를 풀고, 여기에 n 을 더해서 그 답을 찾을 수 있습니다. 즉,
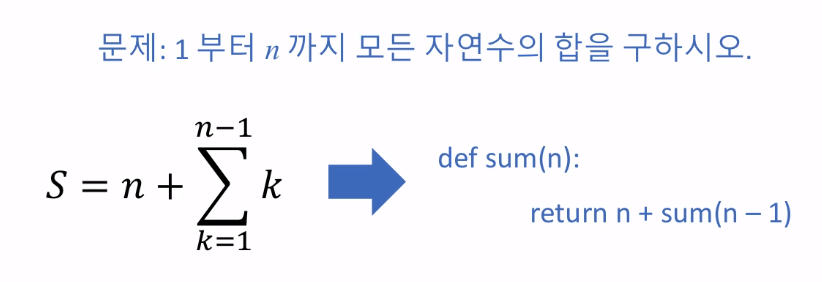
sum(n) = sum(n - 1) + n
입니다.

1부터 n까지 구하는 문제를 구해보겠습니다. 위와 같이 식이 변경이 됩니다.
우측에 있는 그림을 식으로 쓰면
아래와 같이 됩니다.
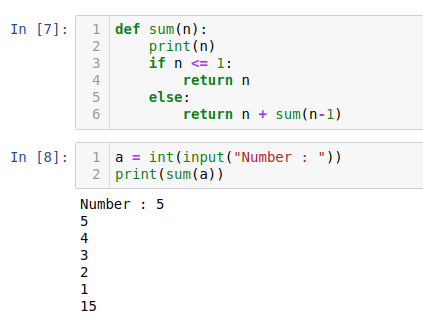
n이 계속 작아진다면 음수가 되서도 진행되니깐
조건문으로 종결을 꼭 시켜줘야 합니다.
재귀 호출은 종결 조건이 반드시 필요합니다.
recursive function 이외에
iterative 으로도 구현해보겠습니다.
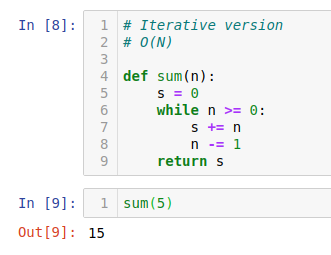
빅오 N 만큼의 시간복잡도를 가졌습니다.
iterative 는 하나의 sum의 대상이 될 변수를 선언해서 거기다 n을 더하고 -1 을 빼면서 다시 더해줍니다.
재귀함수를 공부할 때는 recursive 와 iterative 2가지 형태 모두 구현하는 것이 좋습니다.
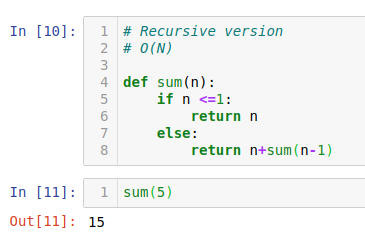
Recursive 버전과 iterative 버전을 비교하면서 방식을 음미해보시길 바랍니다!
정리하겠습니다.
모든 재귀 호출에 대해 재귀 하수는 인수, 반환 주소, 지역 변수를 메모리의 스택에 할당합니다. 이러한 데이터를 스택에 넣고(push) 꺼내는(pop) 데에는 시간이 소비됩니다. 재귀 알고리즘은 최소 O(n)의 공간을 사용합니다. 여기서 n은 재귀 호출의 깊이(depth)입니다.
재귀는 계산이 중복되거나 하위 문제가 겹치는경우 비용이 많이 듭니다. 어떤 경우에는 스택 오버플로가 발생할 수도 있습니다. 이러한 이유로 하위 문제가 겹치는 경우에는 반복문을 사용하는 것(iterative)이 더 좋은 방법이 될 수 있습니다.
연습문제 - 피보나치 수열
인자로 0 또는 양의 정수인 x 가 주어질 때, Fibonacci 순열의 해당 값을 구하여 반환하는 함수 solution() 을 완성하세요.
Fibonacci 순열은 아래와 같이 정의됩니다.
F0 = 0
F1 = 1
Fn = Fn - 1 + Fn - 2, n >= 2

먼저 재귀적으로 피보나치를 구현해보았습니다. 맨 아래에 어떻게 구현되는지 이해를 위해 풀어써 써보았습니다.
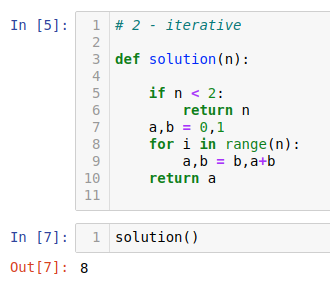
이번에는 반복문으로 풀어보았습니다.
시간복잡도는 반복문으로 푼 것이 더 낫습니다.
예제를 몇 개 더 보겠습니다.
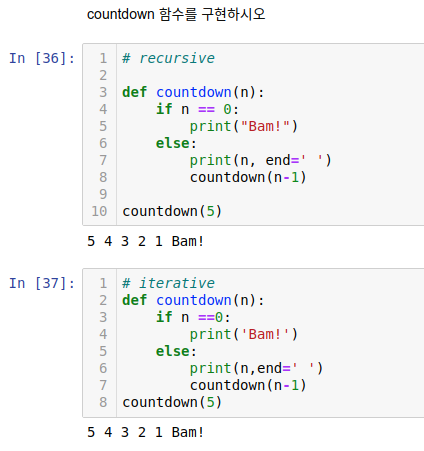
1. countdown 만들기
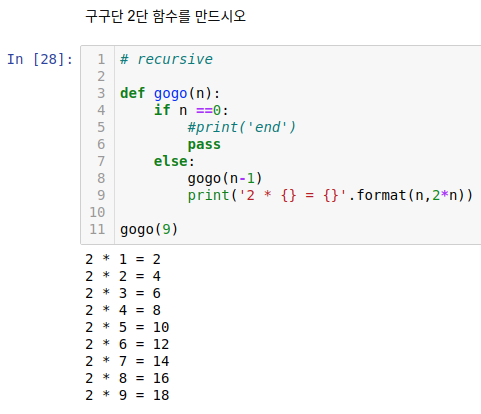
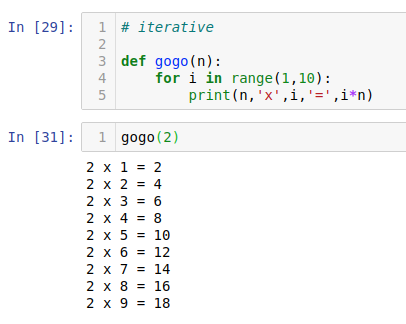
2. 구구단 2단 함수를 만드시오
3. 팩토리얼을 구현하시오
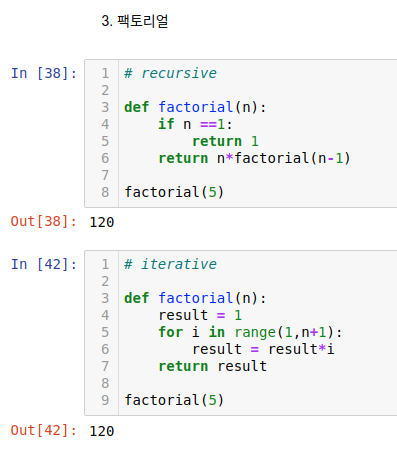
이정도로 재귀함수 기초를 마치겠습니다 :)